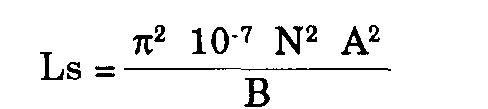
RAPPELS SUR LA REALISATION DES BOBINAGES
Olivier ERNST F5LVG
Retour sur la page d'accueil : de multiples autres documents sur la radio vous attendent
L'emploi des bobinages est fréquent dans les réalisations d'amateurs. S'il existait autrefois des bobinages dans le commerce, ce n'est plus le cas aujourd'hui. Heureusement il est possible de réaliser facilement des bobines de bon rendement avec des éléments simples. Nous verrons successivement la forme à donner aux bobinages, les supports à employer, la fixation des spires, et enfin le calcul du nombre de spires.
I FORMES À DONNER AUX BOBINAGES
Toutes les formes ont été essayées dans le passé. En fait, il ne reste que les bobinages réalisés sur des mandrins cylindriques, les spires étant en vrac (en nid d'abeille pour le professionnel) ou jointives. Sauf en émission, au-dessus de 8 spires je réalise tous mes bobinages en vrac. Le diamètre du fil à employer en réception est de 2/10 à 4/10 de mm jusque 30 MHz, puis au-dessus de 6/10 à 8/10. Pour simplifier les calculs on assimile le diamètre d d'un bobinage à celui de son mandrin.
Il est aussi important de connaître la longueur 1 du bobinage. Les bobinages de meilleure qualité sont ceux dont le rapport 1/d est compris entre 0,5 et 1,5. Si on peut tolérer un rapport l/d nettement inférieur à 0,5 il ne faut pas dépasser, en sens inverse, un rapport de 2 au risque d'avoir un très mauvais rendement.
II LE RENDEMENT
L'idéal est d'employer des mandrins en plastique. Grâce au système d on peut en avoir de tous diamètres : les corps de stylo-bille transparent (8 mm) ; les tubes d'électriciens (12 à 20 mm) ; les tubes d'évacuation d'eau en PVC (3 à 4 cm). Ces tubes peuvent être collés au support ou être fixés par une tige filetée en PVC (pas métallique). Pour les corps de stylo-bille on peut aussi employer une courte vis métallique de diamètre 4 mm qui ne rentre que dans l'extrémité du tube. Les spires sont enroulées le plus souvent en vrac sur le mandrin non fixé. Il faut les serrer assez fort sur le mandrin pour que la bobine soit stable. Une fois le montage terminé et mis au point on colle les spires avec de la colle liquide transparente (type papeterie). Il faut attendre 12 heures pour que la colle soit sèche. Au-dessus de 50 MHz j'utilise du fil rigide sans mandrin.
III CALCUL DU NOMBRE DE SPIRES (formule précise)
Il existe une formule simple qui mérite quelques explications avant d'être donnée. La bobine la plus simple, du point de vue théorique, est un solénoïde, c'est-à-dire que son diamètre est petit par rapport à sa longueur. On démontre que son inductance Ls est :
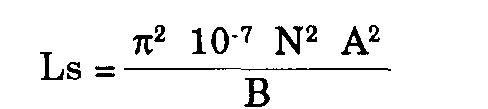
avec Ls inductance en Henry, N le nombre de spires, A le diamètre de la bobine (de section circulaire) en mètre, B la longueur de la bobine en mètre.
En pratique le diamètre des bobines n'est pas négligeable, on doit donc introduire un coefficient correcteur k qui a été déterminé expérimentalement. On a :

avec A diamètre de la bobine et B sa longueur.
Au
total l'inductance L d'une bobine de section circulaire est

avec L en Henry, A et B en mètre.
Pour calculer le nombre de spires en fonction de la fréquence de résonance FO et de la capacité d'accord C, d'un circuit oscillant LC, il suffit d'utiliser la formule de Thomson :

Alors on obtient la formule suivante qui donne pour les circuits oscillants le nombre de spires en fonction de la fréquence de résonance, de la capacité d'accord, et du diamètre et la longueur de la bobine :

avec A diamètre de la bobine en centimètre (cm), B longueur de la bobine en cm, C capacité d'accord en Farad (1 PF = 10-12 F), FO fréquence de résonance en Hertz (1 kHz = 1000 Hz).
Il faut signaler que cette formule, dans les conditions normales d'utilisation a 10 % de précision ce qui est excellent. En général le nombre de spires est supérieur de 10% au nombre de spires nécessaire ce qui est préférable car il est plus facile d'enlever des spires que d'en ajouter.
IV CALCUL DU NOMBRE DE SPIRES (formule simplifiée)
Cette formule est basée sur le calcul du coefficient de self induction d’une spire unique. Si le diamètre de la spire est proche de 20 fois le diamètre du fil employé, on a alors :
L = A / 50
L µH, A diamètre en cm
Pour un nombre N de spires il est possible d’envisager 2 cas extrêmes :
- Les spires sont tassées à l’extrême (longueur de la bobine nulle), chaque spire est alors dans le champ magnétique créé par toutes les spires. La self induction est alors proportionnelle au carré du nombre de spires.
- Les spires sont extrêmement espacées les unes les autres(longueur de la bobine infinie), le champ magnétique créé par chaque spire est alors négligeable sur les spires voisines. La self induction est alors directement proportionnelle au nombre de spires.
Ces 2 cas sont théoriques, et ne peuvent être réalisés en pratique ! Dans la réalité, le coefficient de self induction sera donc proportionnel au nombre de spires mis à une puissance comprise entre 1 et 2.
Des essais réels que j’ai réalisés ont montré qu’il fallait prendre le nombre de spires élevé à la puissance 1,66. Par ailleurs, une petite correction empirique m’a fait diminuer la valeur 50 en 45. Le calcul du coefficient de self induction est alors facile :
L = (A / 45) N1,66
L µH, A diamètre en cm, N nombre de tours.
Pour calculer le nombre de spires d’une bobine d’un circuit oscillant, il suffit de faire intervenir la formule de Thomson, et on obtient :
N = (11 105 / Fo2 C A)0,66
avec L µH, A diamètre en cm, C en pF
En pratique cette formule est extrêmement précise quand le diamètre de la bobine est le double de sa longueur, et l’épaisseur de la bobine le vingtième du diamètre. L’épaisseur de la bobine correspond au diamètre du fil pour une bobine simple couche. Pour une bobine multicouche, il faut multiplier le diamètre du fil (gaine comprise) par le nombre de couche. Les résultats restent excellents quand on ne s’écarte pas de plus d’un facteur 2 de ces valeurs. Ils restent acceptables jusqu’à une variation par un facteur 4. En pratique, il s’agit de la seule formule que j’emploie pour réaliser des circuits oscillants en ondes courtes. Son grand intérêt est d’obtenir une bonne précision en ne connaissant que 2 paramètres : la capacité d’accord, et le diamètre du mandrin à disposition. Enfin, une simple calculatrice scientifique suffit pour effectuer facilement le calcul.
V - CONCLUSION
Si les formules décrites sont précises le grid-dip reste utile pour vérifier le résultat. Enfin au-dessus de 30 MHz et même 20 MHz de nombreux éléments incontrôlés (fil de câblage, capacités réparties) viennent modifier de manière imprévisible ces calculs simples. A noter qu'il existe désormais des petites bobines sur le marché ressemblant extérieurement à des résistances. Ces bobines contiennent un noyau de ferrite et ont un coefficient de qualité satisfaisant (Q>50). Pour réaliser des circuits couplés il faut les coller dos à dos avec de la colle cyanolite. La valeur des bobines sera calculée par la formule de Thomson. La stabilité de la ferrite avec la température étant variable selon les fabrications, il ne faut cependant pas les employer dans des oscillateurs LC.
REMARQUE
La formule de Thomson peut être facilement simplifiée. J’emploi donc toujours en pratique la formule suivante :
L = 25000 / Fo2 C
avec L µH, Fo MHz, C en pF.
Cette formule de Thomson ainsi que la formule simplifiée de calcul des circuits oscillants sont affichées en permanence à proximité de ma table de travail. Faites en autant !
Olivier ERNST F5LVG
Retour sur la page d'accueil : de multiples autres documents sur la radio vous attendent